Maximizing
Your Success in Mathematics - by Jim Hoffman
For some success in mathematics seems to come naturally, for others it will
appear to be a battle up one hill after another, and for the rest it will fall
some where in between these two extremes. It does not matter into which group
you fall because your goal is to be the best that you possibly can. To maximize
your potential it is necessary that you address a number of areas:
Note Taking
The starting point is the realization that when material is presented in
class it is a combination of visual presentation and oral communication.
- The visual presentation includes definitions, written explanations, diagrams
and examples. These could be written on the board, shown on an overhead, be
part of a power point presentation, be excerpts from a text, be part of an
internet search or be in the form of handouts.
- The oral communication is material that seeks to explain the visual presentation
in greater detail. This will include relating the material to previously covered
material, identifying key components, identifying major problem areas, presenting
hints to solve a problem or reduce errors and answers to student generated
questions.
What should you do?
- Attend class everyday.
- Take notes. The notes that you take are part of your learning style and
what you include will not necessarily match what someone else deems to be
important. Remember the degree of completeness of notes is usually based on
what you already understand and how comfortable you are with the material
being covered.
For example if the lesson is on the laws of exponents and you do know
the laws and their application you may conclude that all that is necessary
for your notes is a series of examples while another student may require
each law to be written out including a written description of how the
law functions and all the necessary examples.
- Learn to write and listen at the same time. This is not an easy task
because for a period of time your focus must be on what is happening in class.
This is a skill that you must continually work on refining so it becomes second
nature to you. As the teacher is presenting material copy what is being written
on the board or shown by some other means. Listen as the material is orally
explained and include any additional points as part of your written notes.
- It is sometimes more beneficial to write your notes in your own words.
This process forces you to be more involved in the class and will usually
make it easier for you to remember what has been covered.
- A note of warning. If for some reason you tend to daydream, or you are
over tired, or you find it necessary to engage in conversation with someone
you increase the risk of falling behind in writing notes and you will fail
to hear the oral explanations being provided.
- It is important to note that your teacher will formulate or design exam
questions based on the materials and examples covered in class.
- Utilize the two color approach when taking notes. Use a different color
to highlight areas that are identified as important, where errors could possibly
occur and any new terms that are introduced.
- Use the margins of your notebook to direct your attention to an important
example or explanation.
- Actively participate in class. Remember if you do not understand some
part of the lesson there may be others in the same situation and they could
benefit from what you do and say. Bottom line: if you do not understand what
is being presented ask questions. Take a moment or two and use your knowledge
base to develop the question. It is more advantageous for you to frame the
question identifying the area of concern versus saying "I don't understand".
This process allows the teacher to quickly identify what you have trouble
understanding. Examples of questions that could be asked.
- I do not understand why
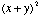 does
not equal
does
not equal 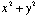 ?
?
- What are the key points in identifying the difference between the
equation of a circle and the equation of an ellipse?
- These are the steps I used when solving the equation
 resulting in a solution of
resulting in a solution of 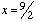 . Where is my mistake?
. Where is my mistake?
- Will you explain why my log equation of
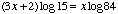 is not correct when compared to the first line
is not correct when compared to the first line 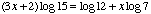 of your solution to the question
of your solution to the question 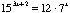 ?
?
- When I convert a percent to a decimal do I move the decimal two places
to the right or two places to the left?
- Can the angle of elevation and the angle of depression be considered
the same since they represent the idea of alternate interior angles?
- What is the difference between a whole number and a natural number?
- Since each class represents only one of many building blocks in a unit
you should review the previous days notes at the start of each lesson. This
process of continual review helps you tie the concepts together and prepares
you to examine the new material being presented.
- At the end of each lesson (or after school) you should review the notes
that you have taken. This is the best time to rewrite in your own words a
quick summary of the keys points. What does this achieve?
- It provides you with the opportunity to identify any areas which you
have difficulty understanding and what points need further clarification
in class the next day.
- It helps you identify any areas that have been omitted or ones in which
you may have made an error.
- It provides you an opportunity to complete any questions that you did
not have time to write out completely during the lesson.
- It provides a quick review resource that you can utilize at the beginning
of the next lesson because each lesson builds on what has been covered the
previous day.
- It provides you an opportunity to link the key concepts of the unit.
- It creates a quick reference guide when preparing for exams.
- Create three special reference pages. One of the pages should highlight
errors that need to be avoided, the second should be a list of all formulae
covered within the course and the third should be a list of definitions categorized
by unit or chapter. The last reference page will be valuable when preparing
for short answer and matching questions on an exam.
- To make your note-taking more efficient it may help if you develop your
own set of abbreviations. Some examples include: "//" - parallel
lines, "iff" - if and only if, "w/o" - without, ">"
- greater than, "D"
- triangle
Clues and Cues Used By Teachers
- To stress items that are important the teacher's voice may become louder
or he may speak a little slower.
- To emphasis certain points the teacher will usually point to the area
of concern.
- If a teacher writes something on the board it should be considered important
and be an integral part of your notes.
- When a teacher repeats certain facts consider them as important and make
sure they are in your notes.
- Listen for phrases that relate to main ideas. These include: The main
point is...., Note this...., Remember this...., The uses are...., The most
common error is ...., This is a major point......
- Listen for the summary at the end of the lesson. This is the point at
which all the key elements of the lesson are revisited. Listen for key words
such as "finally" or "in summary" or "in conclusion".
Assignments/Homework
- The focus of assignments and homework is to provide you with the opportunity
to learn the formulae and techniques that you need to know. In very simple
terms math is learned by doing.
- Homework is an effective learning tool when the work is done promptly.
- To build up an individual's skill level it is essential that assignments
and homework are completed. This means that all questions should be attempted
because these form the framework from which you will decide which concepts/skills
have been mastered and what areas require additional help and explanation.
- When completing an assignment it is necessary to write out complete solutions.
This process serves a number of purposes:
- It allows you to frame your questions it you do not understand a
solution that the teacher may present.
- It provides you with a reference guide to the solution to a number
of questions when preparing for exams.
- It helps you identify special types of questions that could be used
in a chapter or final evaluation.
- When doing homework take time to analyze what you are doing and when
you identify a special skill that is being developed include this as part
of your summary at the end of each lesson.
- Remember that the amount of time that you spend on homework will vary
on the difficulty of the new work and on your skill base.
- Not doing homework and waiting for the work to be covered in class the
next day will provide you with the opportunity to copy out the solution to
the problem but it will not provide you with the essential practice that is
necessary to master a concept.
- Once the homework has been completed and taken up in class take a few
minutes at the end of the class to include in you previous day's lesson summary
a list of questions that you will do when preparing for an exam. Remember
you do have the solutions to these questions. If you do not wish to rewrite
the questions you could create a list of questions by citing each question's
reference number.
- Control the amount of help you request of a teacher but do get help as
soon as possible. It is more advantageous for you to ask for a hint and then
attempt to solve the question by yourself. Make note of the hint because it
is usually one the teacher has found to be effective when encountering this
type of problem. Remember you learn math by doing.
- Use the assigned text as a source of additional examples that may help
you with particular homework questions.
- Remember that when you do homework you are learning a process and not
just how to do a specific problem.
- Taking time to explain a procedure for doing a question to a fellow classmate
serves as an excellent procedure for internalizing the concept for yourself.
- If you have a major assignment one of the best procedures to follow is
to break the assignment into smaller parts. If completing the assignment on
time becomes a problem talk to your teacher in advance of the due date.
- Use the assignment time provided in class to do a select number of questions
that come from different parts of the assignment. This will allow you to develop
reference questions and solutions for the remainder of the questions found
in the assignment.
Problem Solving
This area represents the most important part of a math class. For most individuals
the phrase "problem solving" focuses their attention on word problems
but the actual fact is that problem solving covers a variety of question levels.
These include:
a) Problems that focus on testing memorization or skills:
- Identify a formula:
- the quadratic formula
- the distance formula
- the area formula of a triangle
- the simple interest formula
- the formula for slope of a line
- the standard form of a circle
- Definitions
- line
- prime number
- transversal
- integer
- annuity
- coterminal angle
- Processes (written explanation)
- conversion of a percent to a decimal
- the procedure for completing the trinomial square of a quadratic function
- the steps for factoring the difference of squares
- the steps for simplifying an algebraic expression
- graphing a line using the slope-intercept method
- using Cramer’s rule to solve a system of equations with three
unknowns
- Processes (demonstration of skill)
- convert an integer into a product of prime factors
- calculate the retail cost of an item given wholesale cost and percent
markup
- factor the difference of cubes
- determine the first derivative of the function
- determine the area of the given parallelogram
- determine the slope of the line given two points
b) Problems that require application to familiar situations (sometimes referred
to as template problems)
- graphing linear functions using one of three different methods
- solving a system of equations using the most applicable method
- determining the missing components of right triangles
- simplifying algebraic expressions
- factoring algebraic expressions
- solving money problems
- finding the total area of irregularly shaped structures
- finding the limit of functions
- completing geometric proofs
c) Problems that require the application of skills to unfamiliar situations.
These problems require a multi-step approach involving several different math
skills and techniques.
- proving trig identities
- analyzing equations and sketching the appropriate graph
- solving triangle problems
- determining related rates
- solving problems involving systems of equations
What can you do?
- The greater your experience in math, the more types of problems you will
encounter.
- The more complex the problem, the greater number of steps that will be
required to solve the problem.
- Solving problems require a complete solution. Make every effort to minimize
the quick solution in which you write a few lines and then check the answer
if given at the back of the book or ask a classmate what answer they have
determined.
- If you do not get the right answer do not use this as a signal to move
on to the next question. Use this as the starting point to rework the problem.
It is better to continue to work on a problem until you get it right rather
than doing an entire assignment incorrectly.
- Do not convince yourself that you can do the problem after arriving at
an incorrect solution without reworking the problem.
- Steps for solving a problem:
- make every attempt to understand the problem by identifying what
the problem is asking you to find or solve for. This is best achieved
by reading through the problem at a moderate speed to first get an overview
of the problem. Reread the problem to determine what is being asked and
take the time to express the problem in your own words.
- draw an appropriate labeled diagram
- formulate a plan which identifies the skills and techniques that
you have learned that can be applied to solve the problem.
- form relationships among the given facts. This translates into writing
an algebraic equation containing the unknown
- identify formula that could be used to solve the problem
- use some simple procedures such as guess and test, reasoning and
working backwards to get a better sense of what the problem is asking
- look for patterns within the given problem that could be related
to previously solved problems
- carry out your plan showing all your work (steps)
- break the problem into simpler parts and see if this relates to the
problem as a whole
- check your answer by asking yourself if the determined answer seems
reasonable
- if your plan does not result in a solution to the problem try another
plan. Remember, do not erase what you have done because some of the previous
work could hold clues to what you need to do.
Take a few moments to analyze what you have done because this will now serve
as a framework to solve similar problems. Include in your analysis the following:
what formula and rules were used, what method was successful, how did you start
the problem and does this procedure parallel what has been done with examples
presented in class or found in a textbook.
Test Preparation
- The first element in exam preparation is the completion of all assignments
and homework.
- The best time to get clarification in problem areas is when you first
encounter the difficulty.
- Start studying early because math is not one of the subjects that lends
itself to the concept of cramming.
- Develop a study schedule that will focus your efforts several days before
the exam. If it is a final exam you may want to consider a schedule that includes
several weeks of prep time.
- Ask the teacher to outline the format of the exam.
- If questions are to be asked just prior to an exam they should be of
the type that help explain some minor detail.
- Review all you lesson summaries noting all formulae that have been introduced.
- Check to see that you can still do the homework problems. It is not enough
to look at a question and its solution. Take the time to work out each question
as if they were part of the exam. The list that you prepared for each lesson
serves as an excellent source because if you remember, you do have complete
solutions for each of the problems.
- Use the resources found in the text. At the end of each chapter is a
unit or chapter test with an answer key usually provided at the back of the
text. This serves as an excellent review because it will contain a list of
all the types of questions found in that unit.
- If the teacher provides you with a review sheet make sure that you attempt
each question and come prepared to the next class to ask questions that outline
areas of difficulty. Remember to frame your questions as mentioned above.
- If no review is provided make up your own practice exam using some of
the questions you have identified in your summary notes.
- Once you have worked through the questions and formula applications take
a few minutes to write out a summary of the types of questions you have learned
to solve, the key techniques that you used and how to identify which technique
is applicable to which problem. This summary will also serve as a study guide
when preparing for your final exam.
- One method that may help you internalize problem solving is to use the
concept of talking to yourself. This idea is one in which you explain in your
own words particular solution strategies or create a mental checklist of the
steps that must followed. This idea of talking to yourself provides you with
a mental verbal tool that may help you overcome a confusing part of a question.
- Use flashcards as a study aid for definitions and formulae.
- Use previous exams and quizzes as study tools when preparing for the
final exam.
- Get a sufficient amount of rest prior to the test. Math tests are easier
when you are mentally sharp.
Test Taking
In General:
- Look over the entire test to get a sense of length and identify which
questions you know how to do and which ones will require more effort on your
part.
- The order in which you do the test is entirely up to you. The sequence
that is recommended is as follows:
- Do the problems that you know for sure you can complete as this
will build up your confidence.
- Tackle the questions that you feel you can possibly solve
- Try the questions that you are least sure about.
- Take the time to read each question carefully and do all the parts of
the question.
- Verify your answers by asking yourself whether or not the answer that
you have determined makes sense.
- If you finish early check each problem or as many as time will allow.
- Do not let the speed at which others finish the exam influence you and
your approach to writing the exam.
- Time is a critical component on an exam. It is recommended that you work
quickly and continuously but with attention paid to legible writing and the
necessity of showing all your work. If you get stuck on a particular problem
leave it and move on to the next. Remember that when you work on another question
it may provide you with the necessary information to solve the problem that
you had left.
- Do not spent a lot of time on questions that have been assigned low marks.
Working on the questions that you know you can solve will provide you with
extra time to tackle the more difficult questions.
- Show you work. This provides you with the opportunity to demonstrate
to the teacher how much you do know and allows the teacher to assign partial
marks based on your work.
- It is strongly suggested that you draw a line through rather than erase
something that you feel is incorrect. Why:
- Erasing takes time
- You may erase some information that could be useful later on
- Partial marks could be assigned if you do not complete the question
- If you run out of space place your answer on another sheet.
- If the problem is one that is made up multiple steps it may help to create
a brief outline of the steps before actually solving the problem.
- Analyze your test when it is returned to you. This process will help
you establish some future guidelines. These include:
- did the questions come from lectures, from homework or from some
other source
- how were the problems different from the ones you have done in homework
assignments or from those presented in lectures
- where was the greatest source of errors - careless errors, lack of
time, lack of understanding of presented material, uncertainty of what
mathematical procedures to use or lack of exam preparation
- what must be changed to adjust for the errors that were made.
Multiple Choice Questions:
- Although the general tendency is to look over the choices immediately
after reading the question this practice should be avoided and you should
try answering the question before considering the various alternatives. The
idea of working out the question first focuses your attention on a possible
correct choice and reduces both the "guess factor" and trying to
make an answer work for a particular question.
- Once a selection has been made do not rush on to the next question. Consider
each of the answers and the reason why each of the others should not be considered.
If a question requires a lot of computation mark the question and come back
to it if time permits . Rework the question on a separate piece of paper and
compare this answer with your original.
- If you are not sure of the answer it may help to try and rephrase the
original question. The idea of rephrasing is part of the mental exercise of
talking to yourself and during this process some verbal clue may focus your
attention on a possible correct solution.
- If you encounter a question that forces you into a guessing situation
try to eliminate the most unlikely choices.
- The bottom line is that you must remember that the question and
its respective choices have been designed to take into account all the possible
errors you may make when solving the question.
Matching Questions
- Read all the items in both columns before answering any of the questions
- Answer the questions that you know first.
- Cross out the letter that you have used so that you can easily see what
is left.
- Leave the most difficult questions to the last and then analyze each
item and decide which has the best fit.
- Do not leave any question without an answer. If all else fails make a
guess.
References
1. Success in Mathematics, Department of Mathematics and Computer
Science, Saint Louis University, 1993
2. How to Study Math and Science, The U T Learning Center, The University
of Texas at Austin, 2003
3. Math Study Skills, Learning Skills Center of the Student Counseling
Service, UC Berkeley, 1999
4. Taking Objective Tests, University Learning Center, University
of North Dakota, 2002, www.und.edu/dept/ULC/rf.objt.htm
5. General Note Taking Guidelines, University Learning Center, University
of North Dakota, 2002, www.und.edu/dept/ULC/rf-gn-nt.htm
6. General Listening Guidelines, University Learning Center, University
of North Dakota, 2002, www.und.edu/dept/ULC/rf-lstng.htm
7. Learning: Study Skills, Student Affairs, University of Toronto,
2001, www.sa.utoronto.ca/handbook.php
8. Building Study Skills, Stanford Medical Youth Science Program,
2000, www.med.stanford.edu/school/smysp/nojava/preparation.html
9. What Can Be Done About Listening, Academic Skills Center, Dartmouth
College, 2001
10. Learning By Listening, Academic Skills Center, Dartmouth College,
2001
11. Ten Steps To Academic Success, Academic Skills Center, Dartmouth
College, 2001
12. Homework Suggestions, Student Advice Web Pages, 2000. www.math.uion.edu/~dpvc/courses/advice/hm.html
13. Hints on Studying For Exams, Student Advice Web Pages, 2000.
www.math.uion.edu/~dpvc/courses/advice/study.html
14. Notetaking Tips, University Learning Center, University of North
Dakota, 1997, www.und.edu/dept/ULC/rf.nttip.htm
15. Hints On How To Study, www.uic.edu/classes/phar/phar332/how to
study
16. Studying For Tests, Homework Center: Study Skills, 2004, www.infoplease.com/homework/studyskills4.html
17. Getting Ready For Your Math Final, Study Guides and Test-Taking
Strategies, www.eop.mu.edu/study/MathFinal.html
18. Math Study Skills, Math Study Skills - Tips, math.bigattitude.com/mathtips.html

